numops Namespace Reference

Namespace containing functions related to operations on numbers and other datatypes. More...

Classes
struct	CoordinatePoint
	This struct represents a point in a 3D coordinate system. More...

Functions
template<typename T >
constexpr T	Clamp (T tValue, T tMin, T tMax)
	Clamps a given value from going above or below a given threshold.
template<typename T >
bool	Bounded (T tValue, T tMin, T tMax, const bool bInclusive=true)
	Checks if a given value is between the given maximum and minimum ranges.
template<typename T >
constexpr T	MapRange (const T tValue, const T tOldMinimum, const T tOldMaximum, const T tNewMinimum, const T tNewMaximum)
	Maps a value to a new range given the old range.
template<typename T >
constexpr T	InputAngleModulus (T tValue, T tMinValue, T tMaxValue)
	Calculates the modulus of an input angle.
template<typename T >
constexpr T	AngularDifference (T tFirstValue, T tSecondValue)
	Calculates the distance in degrees between two angles. This function accounts for wrap around so that the most acute or smallest radial distance between the two points is returned. The distance is positive if going from the first angle to the second angle results in clockwise motion.
template<typename T >
constexpr void	CoordinateFrameRotate3D (std::vector< CoordinatePoint< T > > &vPointCloud, const double dXRotationDegrees, const double dYRotationDegrees, const double dZRotationDegrees)
	This method will rotate a list of 3D coordinate points a variable amount of degrees around the X, Y, and Z axis in a standard coordinate plane. Any amount of points can be given and any angle of rotation can be given for each individual X, Y, and Z axis as long as the points all share the same coordinate system.

Detailed Description

Namespace containing functions related to operations on numbers and other datatypes.

Author

ClayJay3 (clayt.nosp@m.onra.nosp@m.ycowe.nosp@m.n@gm.nosp@m.ail.c.nosp@m.om)

Date

2023-07-06

Function Documentation

Clamp()

template<typename T >

constexpr T numops::Clamp ( T  tValue, T  tMin, T  tMax  )

inlineconstexpr

Clamps a given value from going above or below a given threshold.

Template Parameters

T	- Template argument for given value type.

Parameters

tValue	- The value to clamp.
tMin	- Minimum value quantity.
tMax	- Maximum value quantity.

Returns

constexpr T - The clamped value.

Author

Eli Byrd (edbgk.nosp@m.k@ms.nosp@m.t.edu), ClayJay3 (clayt.nosp@m.onra.nosp@m.ycowe.nosp@m.n@gm.nosp@m.ail.c.nosp@m.om)

Date

2023-06-20

    {
        return std::max(std::min(tMax, tValue), tMin);
    }

Here is the caller graph for this function:

Bounded()

template<typename T >

bool numops::Bounded ( T  tValue, T  tMin, T  tMax, const bool  bInclusive = true  )

inline

Checks if a given value is between the given maximum and minimum ranges.

Template Parameters

T	- Template argument for given value type.

Parameters

tValue	- The value to check.
tMin	- The minimum bound for the value to be valid.
tMax	- The maximum bound for the value to be valid.

Returns

true - The value is within the bounds.

false - The value is not within the bounds.

Author

clayjay3 (clayt.nosp@m.onra.nosp@m.ycowe.nosp@m.n@gm.nosp@m.ail.c.nosp@m.om)

Date

2023-10-16

    {
        // Check if value is inclusive or not.
        if (bInclusive)
        {
            // Return true if the given value is valid.
            return (tValue >= tMin) && (tValue <= tMax);
        }
        else
        {
            // Return true if the given value is valid.
            return (tValue > tMin) && (tValue < tMax);
        }
    }

Here is the caller graph for this function:

MapRange()

template<typename T >

constexpr T numops::MapRange ( const T  tValue, const T  tOldMinimum, const T  tOldMaximum, const T  tNewMinimum, const T  tNewMaximum  )

inlineconstexpr

Maps a value to a new range given the old range.

Template Parameters

T	- Template value specifying the type of the number to map to new range.

Parameters

tValue	- The value to remap.
tOldMinimum	- The current range's minimum value.
tOldMaximum	- The current range's maximum value.
tNewMinimum	- The new range's minimum value.
tNewMaximum	- The new range's maximum value.

Returns

constexpr T - The resultant templated type mapped to the new range.

Author

clayjay3 (clayt.nosp@m.onra.nosp@m.ycowe.nosp@m.n@gm.nosp@m.ail.c.nosp@m.om)

Date

2023-09-22

    {
        // Check if the ranges are valid.
        if (tOldMinimum == tOldMaximum || tNewMinimum == tNewMaximum)
        {
            // Submit logger message.
            std::cerr << "MAPRANGE: The old/new range is not valid." << std::endl;
 
            // Return old, given value.
            return tValue;
        }
 
        // Perform the mapping using linear interpolation.
        T tOldValueRange = tOldMaximum - tOldMinimum;
        T tNewValueRange = tNewMaximum - tNewMinimum;
        T tScaledValue   = (tValue - tOldMinimum) / tOldValueRange;
 
        // Return new mapped value.
        return tNewMinimum + tScaledValue * tNewValueRange;
    }

Here is the caller graph for this function:

InputAngleModulus()

template<typename T >

constexpr T numops::InputAngleModulus ( T  tValue, T  tMinValue, T  tMaxValue  )

inlineconstexpr

Calculates the modulus of an input angle.

Template Parameters

T	- Template value specifying the type of the number to find modulus of.

Parameters

tValue	- Input value to wrap.
tMinValue	- The minimum value expected from the input. INCLUSIVE
tMaxValue	- The maximum value expected from the input. NOT INCLUSIVE

Returns

constexpr T - The wrapped value.

Author

clayjay3 (clayt.nosp@m.onra.nosp@m.ycowe.nosp@m.n@gm.nosp@m.ail.c.nosp@m.om)

Date

2023-10-19

    {
        // Determine the correct modulus number.
        T tModulus = tMaxValue - tMinValue;
 
        // Wrap input if it's above the maximum input.
        int nNumMax = (tValue - tMinValue) / tModulus;
        tValue -= nNumMax * tModulus;
        // Wrap input if it's below the minimum input.
        int nNumMin = (tValue - tMaxValue) / tModulus;
        tValue -= nNumMin * tModulus;
 
        // Check if the final value is the max value, set to min.
        if (tValue == tMaxValue)
        {
            tValue = tMinValue;
        }
 
        // Return wrapped number.
        return tValue;
    }

Here is the caller graph for this function:

AngularDifference()

template<typename T >

constexpr T numops::AngularDifference ( T  tFirstValue, T  tSecondValue  )

inlineconstexpr

Calculates the distance in degrees between two angles. This function accounts for wrap around so that the most acute or smallest radial distance between the two points is returned. The distance is positive if going from the first angle to the second angle results in clockwise motion.

Template Parameters

T	- Template value specifying the type of the number to find difference of.

Parameters

tFirstValue	- The first value.
tSecondValue	- The second value. This will be subtracted from the first value.

Returns

constexpr T - The smallest angular distance.

Note

This function expects the two values to be between 0-360.

Author

clayjay3 (clayt.nosp@m.onra.nosp@m.ycowe.nosp@m.n@gm.nosp@m.ail.c.nosp@m.om)

Date

2024-04-03

    {
        // Calculate the difference between the two angles.
        T tDifference = tSecondValue - tFirstValue;
        // Wrap the difference around the 0-360 degree range.
        tDifference = InputAngleModulus(tDifference, -180.0, 180.0);
 
        return tDifference;
    }

Here is the call graph for this function:

Here is the caller graph for this function:

CoordinateFrameRotate3D()

template<typename T >

constexpr void numops::CoordinateFrameRotate3D ( std::vector< CoordinatePoint< T > > &  vPointCloud, const double  dXRotationDegrees, const double  dYRotationDegrees, const double  dZRotationDegrees  )

inlineconstexpr

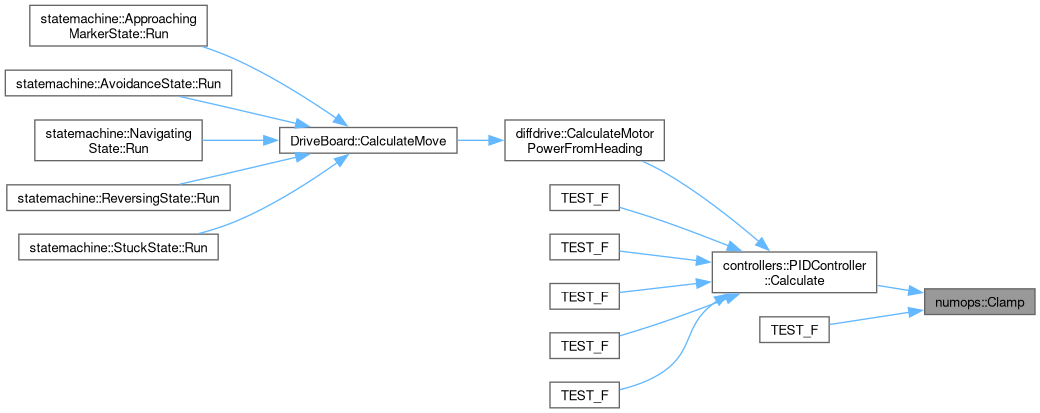
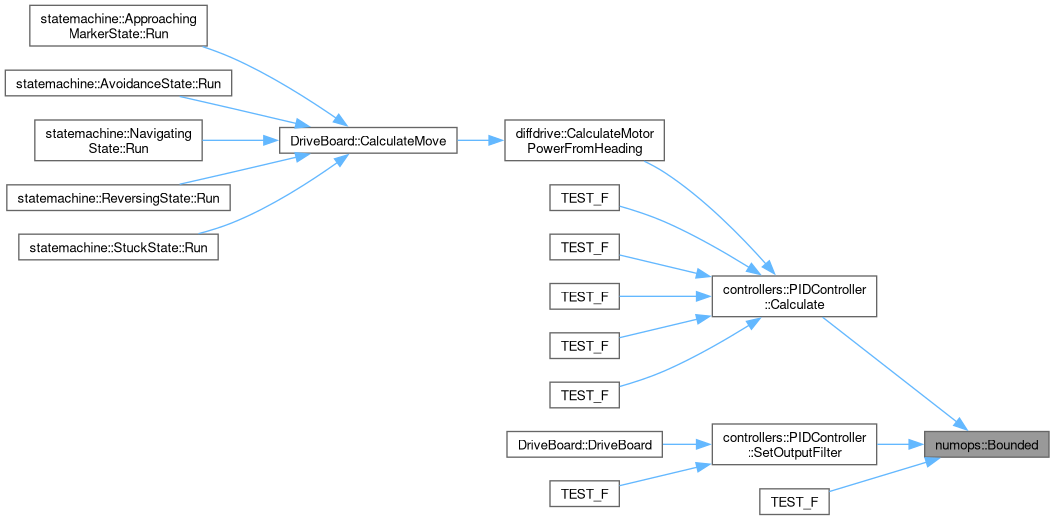
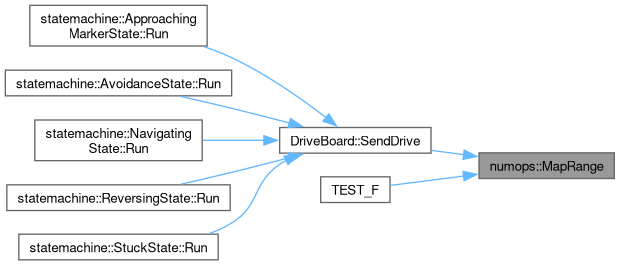
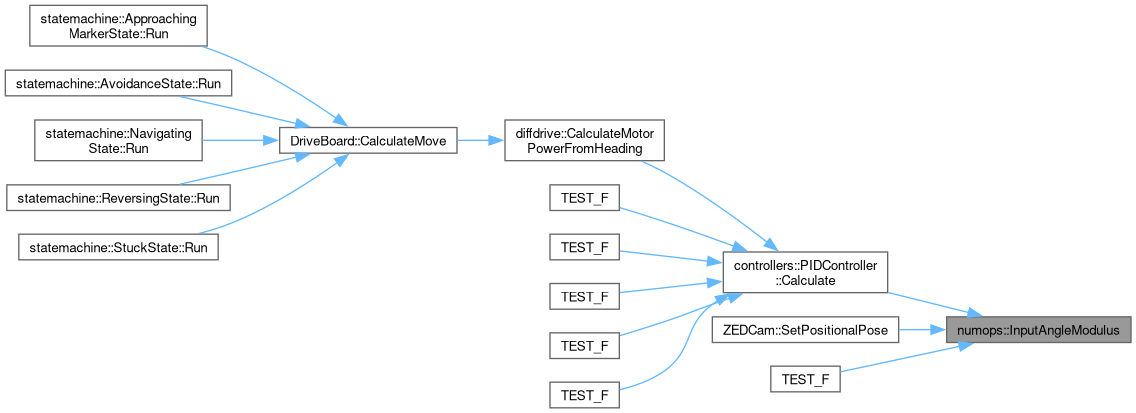
This method will rotate a list of 3D coordinate points a variable amount of degrees around the X, Y, and Z axis in a standard coordinate plane. Any amount of points can be given and any angle of rotation can be given for each individual X, Y, and Z axis as long as the points all share the same coordinate system.

The math for this is based off of these website links for a general 3D cartesian coordinate rotation.

• https://en.wikipedia.org/wiki/Rotation_matrix#In_three_dimensions
• https://www.ni.com/docs/en-US/bundle/labview-api-ref/page/vi-lib/analysis/coordinate-llb/3d-cartesian-coordinate-rotation-euler-vi.html

Each X, Y, and Z component of a point are affected by the new rotation around the X, Y, and Z axis in that order. (Note that any other order of rotations can result in different resultant point locations, so keep that in mind when setting parameters.) Because each cartesian component is affected by each axis' rotation, we can represent the rotation of the point in terms of the following three matrices:

            [1      0           0     ]
Rx(theta) = [0  cos(theta) -sin(theta)]
            [0  sin(theta)  cos(theta)]

            [cos(theta) 0   sin(theta)]
Ry(theta) = [0          1       0     ]
            [-sin(theta) 0  cos(theta)]

            [cos(theta) -sin(theta)  0]
Rz(theta) = [sin(theta)  cos(theta)  0]
            [0             0         1]

Finally multiply each point by the determinate of each of these matrices multiplied together to get the new point after being rotated around each axis.

[X] [X] [Y] = A * [Y] [Z`] [Z]

(Where A is Rz(theta) * Ry(theta) * Rx(theta); X, Y, Z are the original points; X, Y, Z` are the new points.)

So for example, rotating point [1, 0, 0] 90 degrees around the Z-axis would result in this point:

| 0 -1 0 | |1| |0| | 1 0 0 | * |0| = |1| | 0 0 1 | |0| |0|

Template Parameters

T	- The data type of the values stored in the CoordinatePoint struct.

Parameters

vPointCloud	- A reference to a vector of CoordinatePoint<T> structs used to store the X, Y, and Z values of each point. This will contain the rotated modified points after this function completes.
dXRotationDegrees	- The degree amount to rotate the points around the x-axis.
dYRotationDegrees	- The degree amount to rotate the points around the y-axis.
dZRotationDegrees	- The degree amount to rotate the points around the z-axis.

Note

Rotation will happen the the order of X-axis, Y-axis, Z-axis with the positive angle direction being clockwise when looking from the origin and looking down the vector arrow.

Author

clayjay3 (clayt.nosp@m.onra.nosp@m.ycowe.nosp@m.n@gm.nosp@m.ail.c.nosp@m.om)

Date

2024-04-21

    {
        // Convert input degrees to radians.
        double dXRotationRadians = (dXRotationDegrees * M_PI) / 180.0;
        double dYRotationRadians = (dYRotationDegrees * M_PI) / 180.0;
        double dZRotationRadians = (dZRotationDegrees * M_PI) / 180.0;
 
        // Find the cosine and sine for the X-axis rotation matrix.
        double dCosA = cos(dXRotationRadians);
        double dSinA = sin(dXRotationRadians);
        // Find the cosine and sine for the Y-axis rotation matrix.
        double dCosB = cos(dYRotationRadians);
        double dSinB = sin(dYRotationRadians);
        // Find the cosine and sine for the Z-axis rotation matrix.
        double dCosC = cos(dZRotationRadians);
        double dSinC = sin(dZRotationRadians);
 
        // Calculate the 3D rotation matrix using matrix multiplication with proper Euler angles Z, Y, X. A = (Rz * Ry * Rx).
        // First row of A matrix.
        double dAXX = dCosC * dCosB;
        double dAXY = dCosC * dSinB * dSinA - dSinC * dCosA;
        double dAXZ = dCosC * dSinB * dCosA + dSinC * dSinA;
        // Second row of A matrix.
        double dAYX = dSinC * dCosB;
        double dAYY = dSinC * dSinB * dSinA + dCosC * dCosA;
        double dAYZ = dSinC * dSinB * dCosA - dCosC * dSinA;
        // Third row of A matrix.
        double dAZX = -dSinB;
        double dAZY = dCosB * dSinA;
        double dAZZ = dCosB * dCosA;
 
        // Loop through each point in the given point cloud.
        for (CoordinatePoint<T>& stPoint : vPointCloud)
        {
            // Rotate the points in X, Y, Z order using the rotation matrix A.
            T tX = static_cast<T>((dAXX * stPoint.tX) + (dAXY * stPoint.tY) + (dAXZ * stPoint.tZ));
            T tY = static_cast<T>((dAYX * stPoint.tX) + (dAYY * stPoint.tY) + (dAYZ * stPoint.tZ));
            T tZ = static_cast<T>((dAZX * stPoint.tX) + (dAZY * stPoint.tY) + (dAZZ * stPoint.tZ));
            // Update point cloud.
            stPoint.tX = tX;
            stPoint.tY = tY;
            stPoint.tZ = tZ;
        }
    }

Here is the call graph for this function:

Here is the caller graph for this function: